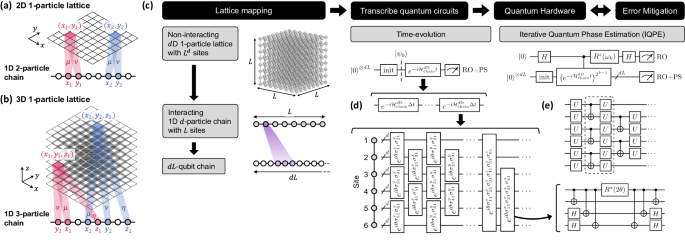
Mapping higher-dimensional lattices to 1D quantum chains

While small quasi-1D and 2D systems have been simulated on digital quantum computers^27,28, the explicit simulation of higher-dimensional lattices remains elusive. Directly simulating a d-dimensional lattice of width L along each dimension requires ~L^d qubits. For large dimensionality d or lattice size L, this quickly becomes infeasible on NISQ devices, which are significantly limited by the number of usable qubits, qubit connectivity, gate errors, and decoherence times.

To overcome these hardware limitations, we devise an approach to exploit the exponentially large many-body Hilbert space of an interacting qubit chain. The key inspiration is that most local lattice models only access a small portion of the full Hilbert space (particularly non-interacting models and models with symmetries), and an L^d-site lattice can be consistently represented with far fewer than L^d qubits. To do so, we introduce an exact mapping that reduces d-dimensional lattices to 1D chains hosting d-particle interactions, which is naturally simulable on a quantum computer that accesses and operates on the many-body Hilbert space of a register of qubits.

General mapping formalism

At a general level, we consider a generic d-dimensional n-band model \({{{{{{{\mathcal{H}}}}}}}}={\sum}_{{{{{{{{\bf{k}}}}}}}}}{{{{{{{{\bf{c}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}^{{{{\dagger}}} }{{{{{{{\mathcal{H}}}}}}}}({{{{{{{\bf{k}}}}}}}}){{{{{{{{\bf{c}}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\) on an arbitrary lattice. In real space,

where we have associated the band degrees of freedom to a sublattice structure γ, and \({h}_{{{{{{{{\bf{r}}}}}}}}{{{{{{{{\bf{r}}}}}}}}}^{{\prime} }}^{\gamma {\gamma }^{{\prime} }}=0\) for \(| {{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}^{{\prime} }|\) outside the coupling range of the model, i.e., adjacent sites for a nearest-neighbor (NN) model, next-adjacent for next-NN, etc. The operator c_rγ annihilates particle excitations on sublattice γ of site r.

To take advantage of the degrees of freedom in the many-body Hilbert space, our mapping is defined such that the hopping of a single particle on the original d-dimensional lattice from \(({{{{{{{{\bf{r}}}}}}}}}^{{\prime} },\;{\gamma }^{{\prime} })\) to (r, γ) becomes the simultaneous hopping of d particles, each of a distinct species, from locations \(({r}_{1}^{{\prime} },\ldots,{r}_{d}^{{\prime} })\) to (r₁,…, r_d) and sublattice \({\gamma }^{{\prime} }\) to γ on a 1D interacting chain. Explicitly, this map is given by

where r_α is the αth component of r, and \( \{ \omega^{\alpha}_{\ell \gamma} \}_{\alpha = 1}^{d}\) represents d excitation species hosted on sublattice γ of site ℓ on the interacting chain, yielding

In the single-particle context, exchange statistics is unimportant, and {ω^α} can be taken to be commuting. This mapping framework accommodates any lattice dimension and geometry, and any number of bands or sublattice degrees of freedom. As the mapping is performed at the second-quantized level, any one-body Hamiltonian expressed in second-quantized form can be treated, which encompasses a wide variety of single-body topological phenomena of interest. We refer readers to Supplementary Note 1 for a more expansive technical discussion. With slight modifications, this mapping can also be extended to admit interaction terms in the original d-dimensional lattice Hamiltonian, although we do not explore them further in this work.

Mapping HOT lattices onto 1D qubit chains

For concreteness, we specialize our Hamiltonian to HOT systems henceforth and shall detail how our mapping enables them to be encoded on quantum processors. The simplest square lattice with HOT corner modes²¹ may be constructed from the paradigmatic 1D Su-Schrieffer Heeger (SSH) model²⁹. To allow for sufficient degrees of freedom for topological localization, we minimally require a 2D mesh of two different types of SSH chains in each direction, arranged in an alternating fashion

where c_xy is the annihilation operator acting on site (x, y) of the lattice and \({u}_{{r}_{1}{r}_{2}}^{\alpha }\) takes values of either \({v}_{{r}_{1}{r}_{2}}^{\alpha }\) for intra-cell hopping (odd r₂) or \({w}_{{r}_{1}{r}_{2}}^{\alpha }\) for inter-cell hopping (even r₂), α ∈ {x, y}. Conceptually, we recognize that the 2D lattice momentum space can be equivalently interpreted as the joint configuration momentum space of two particles, specifically, the (1 + 1)-body sector of a corresponding 1D interacting chain. We map c_xy ↦ μ_xν_y, where μ_ℓ and ν_ℓ annihilate hardcore bosons of two different species at site ℓ on the chain. In the notation of Eq. (2), we identify \({\omega }_{\ell }^{1}\,=\,{\omega }_{\ell }^{x}\,=\,{\mu }_{\ell }\) and \({\omega }_{\ell }^{2}\,=\,{\omega }_{\ell }^{y}\,=\,{\nu }_{\ell }\), and the sublattice structure has been absorbed into the (parity of) spatial coordinates. This yields an effective 1D, two-boson chain described by

where \({n}_{\ell }^{\omega }\) is the number operator for species ω at site ℓ of the chain. As written, each term in \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{chain}}}}}}}}}^{{{{{{{{\rm{2D}}}}}}}}}\) represents an effective SSH model for one particular species μ or ν, with the other species not participating in hopping but merely present (hence its number operator). These two-body interactions arising in \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{chain}}}}}}}}}^{{{{{{{{\rm{2D}}}}}}}}}\) appear convoluted, but can be readily accommodated on a quantum computer, taking advantage of the quantum nature of the platform. To realize \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{chain}}}}}}}}}^{{{{{{{{\rm{2D}}}}}}}}}\) on a quantum computer, we utilize 2 qubits to represent each site of the chain, associating the unoccupied, μ-occupied, ν-occupied and both μ, ν-occupied boson states to qubit states \(\left\vert 00\right\rangle\), \(\left\vert 01\right\rangle\), \(\left\vert 10\right\rangle\), and \(\left\vert 11\right\rangle\) respectively. Thus 2L qubits are needed for the simulation, a significant reduction from L² qubits without the mapping, especially for large lattice sizes. We present simulation results on IBM quantum computers for lattice size \(L \sim {{{{{{{\mathcal{O}}}}}}}}(10)\) in the “Two-dimensional HOT square lattice” section.

Our methodology naturally generalizes to higher dimensions. Specifically, a d-dimensional HOT lattice maps onto a d-species interacting 1D chain, and d qubits are employed to represent each site of the chain, providing sufficient many-body degrees of freedom to encode the 2^d occupancy basis states of each site. We write

where α enumerates the directions along which hoppings occur and \({\hat{{{{{{{{\bf{e}}}}}}}}}}_{\alpha }\) is the unit vector along α. As before, the hopping coefficients alternate between inter- and intra-cell values that can be different in each direction. Compactly, \({u}_{{{{{{{{\bf{r}}}}}}}}}^{\alpha }=[1-\pi ({r}_{\alpha })]{v}_{{{{{{{{\boldsymbol{\pi }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{\alpha })}^{\alpha }+\pi ({r}_{\alpha }){w}_{{{{{{{{\boldsymbol{\pi }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{\alpha })}^{\alpha }\) for parity function π, intra- and inter-cell hopping coefficients \({v}_{{{{{{{{\boldsymbol{\pi }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{\alpha })}^{\alpha }\) and \({w}_{{{{{{{{\boldsymbol{\pi }}}}}}}}({{{{{{{{\bf{r}}}}}}}}}_{\alpha })}^{\alpha }\), and r_α are spatial coordinates in non-α directions—see Supplementary Table 1 for details of the hopping parameter values used in this work. Using d hardcore boson species {ω^α} to represent the d dimensions, we map onto an interacting chain via \({c}_{{{{{{{{\bf{r}}}}}}}}}\mapsto {\prod}_{\alpha=1}^{d}{\omega }_{{r}_{\alpha }}^{\alpha }\), giving

where \({\omega }_{\ell }^{\alpha }\) annihilates a hardcore boson of species α at site ℓ of the chain and \({n}_{\ell }^{\alpha }\) is the number operator of species α. In the d = 2 square lattice above, we had r = (x, y) and {ω^α} = {μ, ν}. The highest dimensional HOT lattice we shall examine is the d = 4 tesseract, for which r = (x, y, z, w) and {ω^α} = {μ, ν, η, ξ}. In total, a d-dimensional HOT lattice Hamiltonian has d × 2^d distinct hopping coefficients, since there are d different lattice directions and 2^d−1 distinct edges along each direction, each comprising two distinct hopping amplitudes for inter- and intra-cell hopping. Appropriately tuning these coefficients allows the manifestation of robust HOT modes along the boundaries (corners, edges, etc.) of the lattices—schematics of the various lattice configurations investigated in our experiments are shown in later sections.

Accordingly, the equivalent interacting 1D chain requires dL qubits to realize, an overwhelming reduction from the L^d otherwise needed in a direct simulation of \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{lattice}}}}}}}}}^{dD}\) without the mapping. We remark that such a significant compression is possible because HOT is inherently a single-particle phenomenon. See “Methods” for further details and optimizations of our mapping scheme on the HOT lattices considered, and Supplementary Note 1 for an extended general discussion, including examples of other lattices and models.

Simulation on quantum hardware

With our mapping, a d-dimensional HOT lattice \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{lattice}}}}}}}}}^{d{{{{{{{\rm{D}}}}}}}}}\) with L^d sites is mapped onto an interacting 1D chain \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{chain}}}}}}}}}^{d{{{{{{{\rm{D}}}}}}}}}\) with dL number of qubits, which can be feasibly realized on existing NISQ devices for \(L \sim {{{{{{{\mathcal{O}}}}}}}}(10)\) and d ≤ 4. While the resultant interactions in \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{chain}}}}}}}}}^{d{{{{{{{\rm{D}}}}}}}}}\) are inevitably complicated, below we describe how \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{chain}}}}}}}}}^{d{{{{{{{\rm{D}}}}}}}}}\) can be viably simulated on quantum hardware.

A high-level overview of our general framework for simulating HOT time-evolution is illustrated in Fig. 2. To evolve an initial state \(\left\vert {\psi }_{0}\right\rangle\), it is necessary to implement the unitary propagator \(U(t)=\exp (-i{{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{chain}}}}}}}}}^{d{{{{{{{\rm{D}}}}}}}}}t)\) as a quantum circuit, such that the circuit yields \(\left\vert \psi (t)\right\rangle=U(t)\left\vert {\psi }_{0}\right\rangle\) and desired observables can be measured upon termination. A standard method to implement U(t) is Trotterization, which decomposes \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{chain}}}}}}}}}^{d{{{{{{{\rm{D}}}}}}}}}\) in the spin-1/2 basis and splits time-evolution into small steps (see “Methods” for details). However, while straightforward, such an approach yields deep circuits unsuitable for present-generation NISQ hardware. To compress the circuits, we utilize a tensor network-aided recompilation technique^30,31,32,33. We exploit the number-conserving symmetries of \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{chain}}}}}}}}}^{d{{{{{{{\rm{D}}}}}}}}}\) in each boson species, arising from \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{lattice}}}}}}}}}^{d{{{{{{{\rm{D}}}}}}}}}\) and the nature of our mapping (see “Methods”), to enhance circuit construction performance and quality at large circuit breadths (up to 32 qubits). Moreover, to improve data quality amidst hardware noise, we employ a suite of error mitigation techniques, in particular, readout error mitigation (RO) that approximately corrects bit-flip errors during measurement³⁴, a post-selection (PS) technique that discards results in unphysical Fock-space sectors^30,35, and averaging across machines and qubit chains (see “Methods”).

a, b Mapping of a higher-dimensional lattice to a 1D interacting chain to facilitate quantum simulation on near-term devices. Concretely, a two-dimensional single-particle lattice can be represented by a two-species interacting chain; a three-dimensional lattice can be represented by a three-species chain with three-body interactions. c Overview of quantum simulation methodology: higher-dimensional lattices are first mapped onto interacting chains, then onto qubits; various techniques, such as d Trotterization and e ansatz-based recompilation, enable the construction of quantum circuits for dynamical time-evolution, or IQPE for probing the spectrum. The quantum circuits are executed on the quantum processor, and results are post-processed with RO and PS error mitigations to reduce effects of hardware noise. See “Methods” for elaborations on the mapping procedure, and quantum circuit construction and optimization.

After acting on \(\left\vert {\psi }_{0}\right\rangle\) by the quantum circuit that effects U(t), terminal computational-basis measurements are performed on the simulation qubits. We retrieve the site-resolved occupancy densities \(\rho ({{{{{{{\bf{r}}}}}}}})=\langle {c}_{{{{{{{{\bf{r}}}}}}}}}^{{{{\dagger}}} }{c}_{{{{{{{{\bf{r}}}}}}}}}\rangle=\langle {\prod}_{\alpha=1}^{d}{n}_{{r}_{\alpha }}^{\alpha }\rangle\) on the d-dimensional lattice, and the extent of evolution of \(\left\vert \psi (t)\right\rangle\) away from \(\left\vert {\psi }_{0}\right\rangle\), whose occupancy densities are ρ₀(r), is assessed via the occupancy fidelity

Compared to the state fidelity \({{{{{{{\mathcal{F}}}}}}}}=| \langle {\psi }_{0}| \psi \rangle {| }^{2}\), the occupancy fidelity \({{{{{{{{\mathcal{F}}}}}}}}}_{\rho }\) is considerably more resource-efficient to measure on quantum hardware.

In addition to time evolution, we can also directly probe the energy spectrum of our simulated Hamiltonian \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{chain}}}}}}}}}^{d{{{{{{{\rm{D}}}}}}}}}\) through iterative quantum phase estimation (IQPE)³⁶—see “Methods”. Specifically, to characterize the topology of HOT systems, we use IQPE to probe the existence of midgap HOT modes at exponentially suppressed (effectively zero for L ≫ 1) energies. In contrast to quantum phase estimation^37,38, IQPE circuits are shallower and require fewer qubits, and are thus preferable for implementation on NISQ hardware. As our interest is in HOT modes, we initiate IQPE with maximally localized boundary states that are easily constructed a priori, which exhibit good overlap (>80% state fidelity) with HOT eigenstates, and examine whether IQPE converges consistently towards zero energy. These states are listed in Supplementary Table 2.

Two-dimensional HOT square lattice

As the lowest-dimensional incarnation of HOT lattices, the d = 2 staggered square lattice harbors only one type of HOT mode—zero-dimensional corner modes (Fig. 1a). Previously, such HOT corner modes on 2D lattices have been realized in various metamaterials^39,40 and photonic waveguides⁴¹, but not in a purely quantum setting to-date. Our equivalent 1D hardcore boson chain can be interpreted as possessing interaction-induced topology that manifests in the joint configuration space of the d bosons hosted on the many-body chain. Here, the topological localization is mediated not due to physical SSH-like couplings or band polarization but due to the combined exclusion effects from all its interaction terms. We emphasize that our physically realized 1D chain contains highly non-trivial interaction terms involving multiple sites—the illustrative example in Fig. 3f for an L = 6 chain already contains a multitude of interactions, even though it is much smaller than the L = 10 and L = 16 systems we simulated on quantum hardware. As evident, the \(d \times 2^d = 8\) unique types of interactions, corresponding to the 8 different couplings on the lattice, are mostly non-local; but this does not prohibit their implementation on quantum circuits. Indeed, the versatility of digital quantum simulators in realizing effectively arbitrary interactions allows the implementation of complex interacting Hamiltonian terms, and is critical in enabling our quantum device simulations.

a Ordered eigenenergies on a 10 × 10 lattice for the topologically trivial C0 and nontrivial C2 and C4 configurations. They correspond to 0, 2, and 4 midgap zero modes (red diamonds), as measured via IQPE on a 20-qubit quantum chain plus an additional ancillary qubit; the shaded red band indicates the IQPE energy resolution. The corner state profiles (right insets) and other eigenenergies (black and gray dots) are numerically obtained via ED. Time-evolution of four initial states on a 16 × 16 lattice mapped onto a 32-qubit chain—b, c localized at corners to highlight topological distinction, d localized along an edge, and e delocalized in the vicinity of a corner. Left plots show occupancy fidelity for the various lattice configurations, obtained from ED and quantum hardware (labeled HW), with insets showing the site-resolved occupancy density ρ(x, y) of the initial states (darker shading represents higher density). The right grid shows occupancy density measured on hardware at two later times. States with good overlap with robust corners exhibit minimal evolution. Error bars represent standard deviation across repetitions on different qubit chains and devices. In general, the heavy overlap between an initial state and a HOT eigenstate confers topological robustness, resulting in significantly slowed decay. f Schematic of the interacting chain Hamiltonian, mapped from the parent 2D lattice, illustrated for a smaller 6 × 6 square lattice. The physical sites of the interacting boson chain are colored black, with their many-body interactions represented by colored vertices. Intra- and inter-cell hoppings, mapped onto interactions, are respectively denoted \({v}_{{{{{{{{\boldsymbol{\pi }}}}}}}}}^{\alpha }\) and \({w}_{{{{{{{{\boldsymbol{\pi }}}}}}}}}^{\alpha }\) for axes α \(\in\) {x, y} and parities \({{{{{{{\boldsymbol{\pi }}}}}}}}\in {{\mathbb{Z}}}_{2}^{1}\).

In our experiments, we consider three different scenarios: C0, having no topological corner modes; C2, having two corner modes at corners (x, y) = (1, 1) and (L, 1); and C4, having corner modes on all four corners. These scenarios can be obtained by appropriately tuning the eight coupling parameters in the Hamiltonian (Eq. (4))—see Supplementary Table 1 for parameter values⁴².

We first show that the correct degeneracy of midgap HOT modes can be measured on each of the configurations C0, C2, and C4 on IBM transmon-based quantum computers, as presented in Fig. 3a. For a start, we used a 20-qubit chain, which logically encodes a 10 × 10 HOT lattice, with an additional ancillary qubit for IQPE readout. The number of topological corner modes in each case is accurately obtained through the degeneracy of midgap states of exponentially suppressed energy (red), as measured through IQPE executed on quantum hardware—see “Methods” for details. That these midgap modes are indeed corner-localized is verified via numerical (classical) diagonalization, as in the insets of Fig. 3a.

Next, we demonstrate highly accurate dynamical state evolution on larger 32-qubit chains on quantum hardware. We time-evolve various initial states on 16 × 16 HOT lattices in the C0, C2, and C4 configurations and measure their site-resolved occupancy densities ρ(x, y), up to a final time t = 0.8 when fidelity trends become unambiguous. The resultant occupancy fidelity plots (Fig. 3b–e) conform to the expectation that states localized on topological corners survive the longest, and are also in excellent agreement with reference data from ED. For instance, a localized state at the corner (x₀, y₀) = (1, 1) is robust on C2 and C4 lattice configurations (Fig. 3b), whereas one localized on the (x₀, y₀) = (1, L) corner is robust only on the C4 configuration (Fig. 3c). These fidelity decay trends are corroborated with the measured site-resolved occupancy density ρ(x, y): low occupancy fidelity is always accompanied by a diffused ρ(x, y) away from the initial state, whereas strongly localized states have high occupancy fidelity. In general, the heavy overlap between an initial state and a HOT eigenstate confers topological robustness, resulting in significantly slowed decay; this is apparent from the occupancy fidelities, which remain near unity over time. In comparison, states that do not enjoy topological protection, such as the (1, L)-localized state on the C2 configuration and all initial states on the C0 configuration, rapidly delocalize and decay quickly.

Our experimental runs remain accurate even for initial states that are situated away from the lattice corners, such that they cannot enjoy full topological protection. In Fig. 3d, the initial state at (x₀, y₀) = (2, 1), which neighbors the corner (1, 1), loses its fidelity much sooner than the corner initial state of Fig. 3b, even for the C2 and C4 topological corner configurations. That said, its fidelity evolution still agrees well with ED reference data. In a similar vein, an initial state that is somewhat delocalized at a corner (Fig. 3e) is still conferred a degree of stability when the corner is topological.

Three-dimensional HOT cubic lattice

Next, we extend our investigation to the staggered cubic lattice in 3D, which hosts third-order HOT corner modes (Fig. 1a). These elusive corner modes have to date only been realized in classical platforms⁴³ or in synthetic electronic lattices⁴⁴. Compared to the 2D cases, the implementation of the 3D HOT lattice (Eq. (6)) as a 1D interacting chain (Eq. (7)) on quantum hardware is more sophisticated. The larger dimensionality of the staggered cubic lattice, in comparison to the square lattice, is reflected by a larger density of multi-site interaction terms on the interacting chain. This is illustrated in Fig. 4b for the minimal 4 × 4 × 4 lattice, where the combination of the various d = 3-body interactions gives rise to emergent corner robustness (which appears as up to 3-body boundary clustering as seen on the 1D chain).

a The header row displays energy spectra for the topologically trivial C0 and inequivalent nontrivial C4a, C4b, and C8 configurations. The configurations host 0, 4, and 8 midgap zero modes (red diamonds), as measured via IQPE on an 18-qubit chain plus an ancillary qubit; the shaded red band indicates the IQPE energy resolution. Schematics illustrating the locations of topologically robust corners are shown on the right. Subsequent rows depict the time-evolution of five initial states on a 6 × 6 × 6 lattice mapped onto an 18-qubit chain—localized at a corner, on an edge, on a face, and in the bulk of the cube, and delocalized in the vicinity of a corner. The leftmost column plots occupancy fidelity for the various lattice configurations, obtained from ED and quantum hardware (labeled HW), with insets showing the site-resolved occupancy density ρ(x, y, z) of the initial state (darker shading represents higher density). The central grid shows occupancy density measured on hardware at a later time (t = 0.6), for the corresponding initial state (row) and lattice configuration (column). Error bars represent standard deviation across repetitions on different qubit chains and devices. Again, initial states localized close to topological corners exhibit higher occupational fidelity. b Hamiltonian schematic of the interacting chain realizing a minimal 4 × 4 × 4 cubic lattice. Sites on the chain are colored black; colored vertices connecting to multiple sites on the chain denote interaction terms. Intra- and inter-cell hoppings, mapped onto interactions, are respectively denoted \({v}_{{{{{{{{\boldsymbol{\pi }}}}}}}}}^{\alpha }\) and \({w}_{{{{{{{{\boldsymbol{\pi }}}}}}}}}^{\alpha }\) for axes α \({w}_{{{{{{{{\boldsymbol{\pi }}}}}}}}}^{\alpha }\) {x, y, z} and parities \({{{{{{{\boldsymbol{\pi }}}}}}}}\in {{\mathbb{Z}}}_{2}^{2}\).

On quantum hardware, we implemented 18-qubit chains representing 6 × 6 × 6 cubic lattices in four configurations, specifically, the trivial lattice (C0), two geometrically inequivalent configurations hosting four topological corners (C4a, C4b), and a configuration with all 2³ = 8 topological corners (C8). Similar to the 2D HOT lattice, we first present the degeneracy of zero-energy topological modes (header row of Fig. 4a) with low-energy spectral data (red diamonds) accurately obtained via IQPE.

From the first row of Fig. 4a, it is apparent that initial states localized on topological corners enjoy significant robustness. Namely, the measured site-resolved occupancy densities ρ(x, y, z) (four right columns) indicate that the localization of (x₀, y₀, z₀) = (1, 1, 1) corner initial states on C4a, C4b, and C8 configurations are maintained, and measured occupancy fidelities remain near unity. In comparison, an initial corner-localized state on the C0 configuration, which hosts no topological corner modes, delocalizes quickly. Moving away from the corners, an edge-localized state adjacent to a topological corner is conferred slight, but nonetheless present, stability (second row of Fig. 4a), as observed from the slower decay of the (x₀, y₀, z₀) = (2, 1, 1) state on C4a, C4b, and C8 configurations in comparison to the C0 topologically trivial lattice. This conferred robustness is diminished for states localized further from topological corners, for instance, surface-localized states (third row), and is virtually unnoticeable for states localized in the bulk (fourth row), which decay rapidly for all topological configurations. Initial states that are slightly delocalized near a corner enjoy some protection when the corner is topological, but are unstable when the corner is trivial (fifth row of Fig. 4a). We again highlight the quantitative agreement of our quantum hardware simulation results with theoretical ED predictions.

Four-dimensional tesseract hyperlattice—HOT corner and edge modes

We now turn to our key results—the NISQ quantum hardware simulation of four-dimensional staggered tesseract HOT lattices. A true 4D lattice is difficult to simulate on most experimental platforms, and with a few exceptions⁴⁵, most works to date have relied on using synthetic dimensions^18,46. In comparison, utilizing our exact mapping (Eqs. (6) and (7)) that exploits the exponentially large many-body Hilbert space accessible by a quantum computer, a tesseract lattice can be directly simulated on a physical 1D spin (qubit) chain, with the number of spatial dimensions only limited by the number of qubits. The tesseract unit cell can be visualized as two interlinked three-dimensional cubes (spanned by x, y, z axes) living in adjacent w-slices (Fig. 5). The full tesseract lattice of side length L is then represented as successive cubes with different w coordinates, stacked successively from inside out, with the inner and outer wireframe cubes being w = 1 and w = L slices. Being more sophisticated, the 4D HOT lattice features various types of HOT corner, edge, and surface modes (Fig. 1a); we presently focus on the fourth-order (hexadecapolar) HOT corner modes, as well as the third-order (octopolar) HOT edge modes.

A L = 6 tesseract lattice is illustrated as six cube slices indexed by w and highlighted on a color map. The header row displays energy spectra computed numerically for the topologically trivial C0 and nontrivial C4, C8, and C16 configurations. The configurations host 0, 4, 8, and 16 midgap zero modes (black circles). Schematics on the right illustrate the locations of the topologically robust corners. Subsequent rows depict the time-evolution of three initial states on a 6 × 6 × 6 × 6 lattice mapped onto a 24-qubit chain—localized on a a corner, b an edge, and c a face. The leftmost column plots occupancy fidelity for the various lattice configurations, obtained from ED and quantum hardware (labeled HW), with insets showing the site-resolved occupancy density ρ(x, y, z, w) of the initial state. Central grid shows occupancy density measured on hardware at the final simulation time (t = 0.6), for the corresponding initial state (row) and lattice configuration (column). The color of individual sites (spheres) denotes their w-coordinate and color saturation denotes occupancy of the site; unoccupied sites are translucent. Error bars represent standard deviation across repetitions on different qubit chains and devices. Initial states with less overlap with topological corners exhibit slightly lower stability than their lower dimensional counterparts, as these states diffuse into the more spacious 4D configuration space. d Hamiltonian schematic of the interacting chain realizing a minimal 4 × 4 × 4 × 4 tesseract lattice. Sites on the chain are colored black; colored vertices connecting to multiple sites on the chain denote interaction terms. Intra- and inter-cell hoppings, mapped onto interactions, are respectively denoted \({v}_{{{{{{{{\boldsymbol{\pi }}}}}}}}}^{\alpha }\) and \({w}_{{{{{{{{\boldsymbol{\pi }}}}}}}}}^{\alpha }\) for axes α \(\in\) {x, y, z, w} and parities \({{{{{{{\boldsymbol{\pi }}}}}}}}\in {{\mathbb{Z}}}_{2}^{3}\). To limit visual clutter, only \({v}_{{{{{{{{\boldsymbol{\pi }}}}}}}}}^{\alpha }\) intra-cell couplings are shown; a corresponding set of \({w}_{{{{{{{{\boldsymbol{\pi }}}}}}}}}^{\alpha }\) inter-cell couplings are present in the Hamiltonian but have been omitted from the diagram.

To start, we realized a dL = 4 × 6 = 24-qubit chain on the quantum processor, which encodes a 6 × 6 × 6 × 6 HOT tesseract. The 4-body (8-operator) interactions now come in d × 2^d = 64 types—half of them are illustrated in Fig. 5d, which depicts only the minimal L = 4 case. As discussed in the “Mapping higher-dimensional lattices to 1D quantum chains” section, these interactions are each a product of d − 1 density terms and a hopping process, the latter acting on the particle species that encodes the coupling direction on the HOT tesseract. In generic models with non-axially aligned hopping, these interactions could be a product of up to d hopping processes. As we shortly illustrate, despite the complexity of the interactions, the signal-to-noise ratio in our hardware simulations (Fig. 5a) remains reasonably good.

In Fig. 5, we consider the configurations C0, C4, C8, and C16, which correspond respectively to the topologically trivial scenario and lattice configurations hosting four, eight, and all sixteen HOT corner modes, as schematically sketched in the header row. Similar to the 2D and 3D HOT lattices, site-resolved occupancy density ρ(x, y, z, w) and occupancy fidelities measured on quantum hardware reveal strong robustness for initial states localized at topological corners, as illustrated by the strongly localized final states in the C4, C8, and C16 cases (Fig. 5a). However, their stability is now slightly lower, partly due to the more spacious 4D configuration space into which the state can diffuse, as seen from the colored clouds of partly occupied sites after time evolution. Evidently, the stability diminishes as we proceed to the edge- and surface-localized initial states (Fig. 5b and c).

Next, we investigate a lattice configuration that supports HOT edge modes (or commonly referred to as topological hinge states in literature²²). So far we have seen topological robustness only from topological corner sites (Fig. 5); but with appropriate parameter tuning (see Supplementary Table 1), topological modes can be made to lie along entire edges. This is illustrated in the header row of Fig. 6, where topological modes lie along the y-edges. As our HOT lattices are constructed from a mesh of alternating SSH chains, we expect the topological edges to have wavefunction support (nonzero occupancy) only on alternate sites, consistent with the cumulative occupancy densities of the midgap zero-energy modes. This is corroborated by site-resolved occupancy densities and occupancy fidelities measured on quantum hardware, which demonstrate that initial states localized on sites with topological wavefunction support are significantly more robust (Fig. 6a, b), i.e., (x₀, y₀, z₀, w₀) = (1, 3, 1, L) overlaps with the topological mode on (1, y, 1, L), y ∈ {1, 3, 5} sites and is hence robust, but (1, 2, 1, L) is not. The stability of the initial state is reduced as we move farther from the corner, as can be seen, for instance, by comparing occupancy fidelities and the size of the final occupancy cloud for (1, 1, 1, L) and (1, 3, 1, L) in Fig. 6a, b, which is expected from the decaying y-profile of the topological edge mode. Finally, our measurements verify that surface-localized states do not enjoy topological protection (Fig. 6c) as they are localized far away from the topological edges. It is noteworthy that such measurements into the interior of the 4D lattice can be made without additional difficulty on our 1D qubit chain, but doing so can present significant challenges on other platforms, even electrical (topolectrical) circuits.

Our mapping facilitates the realization of any desired HOT modes, beyond the aforementioned corner mode examples. The header row on the left displays the energy spectrum for a configuration of the tesseract harboring topologically non-trivial edges (midgap mode energies in black). Accompanying schematic highlights alternating sites with topological edge wavefunction support. Subsequent columns present site-resolved occupancy density ρ(x, y, z, w) for a 6 × 6 × 6 × 6 lattice mapped onto a 24-qubit chain, measured on quantum hardware at t = 0 (first row) and final simulation time t = 0.6 (second row), for three different experiments. a A corner-localized state along a topological edge is robust, compared to one along a non-topological edge. b On a topologically non-trivial edge, a state localized on a site with topological wavefunction support is robust, compared to one localized on a site without support. c A surface-localized state far away from the topological edges diffuses into a large occupancy cloud. The bottom leftmost summarizes occupancy fidelities for the various initial states, obtained from ED and hardware (labeled HW). Error bars represent standard deviation across repetitions on different qubit chains and devices.

Resource scaling

Our approach of mapping a d-dimensional HOT lattice onto an interacting 1D chain enabled a drastic reduction in the number of qubits required for simulation, and served a pivotal role in enabling the hardware realizations presented in this work. Here, we further illustrate that employing this mapping for simulation on quantum computers can provide a resource advantage over ED on classical computers, particularly at large lattice dimensionality d or linear size L. For this discussion, we largely leave aside tensor network methods, as their advantage over ED is unclear in the generic setting of lattice dimensionality d > 1, with arbitrary initial states and evolution time (which may generate large entanglement).

To be concrete, we consider simulation tasks of the following broad type: given an initial state \(\left\vert {\psi }_{0}\right\rangle\), we wish to perform time-evolution to \(\left\vert \psi (t)\right\rangle\), and extract the expectation value of an observable O that is local, that is, 〈O〉 is dependent on \({{{{{{{\mathcal{O}}}}}}}}({l}^{d})\) number of sites on the lattice for a fixed neighborhood of radius l independent of L. State preparation or initialization resources for \(\left\vert {\psi }_{0}\right\rangle\) are excluded from our considerations, as there can be significant variations in costs depending on the choice of specification of the state for both classical and quantum methods. Measurement costs for computing 〈O〉, however, are considered. To ensure a meaningful comparison, we assume first-order Pauli-basis Trotterization for the construction of quantum circuits, such that circuit preparation is algorithmically straightforward given a lattice Hamiltonian. As a baseline, classical ED of a d-dimensional, length L system with a single particle generally requires \({{{{{{{\mathcal{O}}}}}}}}({L}^{3d})\) run-time and \({{{{{{{\mathcal{O}}}}}}}}({L}^{2d})\) dense classical storage to complete a task of such a type⁴⁷.

A direct implementation of a generic Hamiltonian using our mapping gives \({{{{{{{\mathcal{O}}}}}}}}(d{L}^{d}\cdot {2}^{d})\) Pauli strings per Trotter step (see “Methods”), where hoppings along each edge of the lattice, extensive in number, are allowed to be independently tuned. However, physically relevant lattices typically host only a systematic subset of hopping processes, described by a sub-extensive number of parameters. In particular, in the HOT lattices we considered, the hopping amplitude \({u}_{{{{{{{{\bf{r}}}}}}}}}^{\alpha }\) along each axis α is dependent only on α and the parities of coordinates r. Noting the sub-extensive number of distinct hoppings, the lattice Hamiltonian can be written in a more favorable factorized form, yielding \({{{{{{{\mathcal{O}}}}}}}}(dL\cdot {2}^{2d})\) Pauli strings per Trotter step (see “Methods”). Decomposing into a hardware gate set, the total number of gates in a time-evolution circuit scales as \({{{{{{{\mathcal{O}}}}}}}}({d}^{2}{L}^{2}\cdot {2}^{2d}/\epsilon )\) in the worst-case for simulation precision ϵ, assuming all-to-all connectivity between qubits. Imposing linear NN connectivity on the qubit chain does not alter this bound. Crucially, there is no exponential scaling of d in L (of form ~L^d), unlike classical ED.

For large L and d, the circuit preparation and execution time can be lower than the \({{{{{{{\mathcal{O}}}}}}}}({L}^{3d})\) run-time of classical ED. We illustrate this in Fig. 7, which shows a qualitative comparison of run-time scaling between the quantum simulation approach and ED. We have assumed execution time on hardware to scale as the number of gates in the circuit \({{{{{{{\mathcal{O}}}}}}}}({d}^{2}{L}^{2}\cdot {2}^{2d}/\epsilon )\), which neglects speed-ups afforded by parallelization of single- or two-qubit gates acting on disjoint qubits⁴⁸. The difference in asymptotic complexities implies a crossover at large L or d beyond which quantum simulation exhibits a growing advantage. The exact crossover boundary is sensitive to platform-specific details such as gate times and control capabilities; given the large spread in gate timescales (≳3 orders of magnitude) across present-day platforms^49,50, and uncertain overheads from quantum error correction or mitigation, we avoid giving definite numerical promises on breakeven L and d values. Classical memory usage is similarly bounded during circuit construction, straightforwardly reducible to \({{{{{{{\mathcal{O}}}}}}}}(dL)\) by constructing and executing gates in a streaming fashion⁵¹, and worst-case \({{{{{{{\mathcal{O}}}}}}}}({2}^{ld})\) during readout to compute 〈O〉, reducible to a constant supposing basis changes to map components of O onto the computational basis of a fixed number of measured qubits can be implemented on the quantum circuits⁵².

Comparison of asymptotic computational time required for the dynamical simulation of d-dimensional, size-L lattice Hamiltonians of similar complexity as our HOT lattices. a With fixed lattice dimension d and increasing lattice size L, the time taken with our approach on a quantum computer (labeled QC) scales with L², rather than the higher power of L^3d through classical ED. b For fixed L and varying d, our approach scales promisingly, scaling like 4^d instead of \({({L}^{3})}^{d}\) for ED. We assume conventional Trotterization for circuit construction, and at large L and d, our mapping and quantum simulation approach can provide a resource advantage over classical numerical methods (e.g., ED).

The favorable resource scaling (run-time and memory), in combination with the modest dL qubits required, suggests promising scalability of our mapped quantum simulation approach, especially in realizing larger and higher-dimensional HOT lattices. We re-iterate, however, that Trotterized circuits without additional optimization remain largely too deep for present-generation NISQ hardware to execute feasibly. The use of qudit hardware architectures in place of qubits can allow shallower circuits⁵³; in particular, using a qudit of local Hilbert space dimension ≥2^d instead of a group of d qubits avoids, to a degree, decomposition of long-range multi-site gates, assuming the ability to efficiently and accurately perform single- and two-qudit operations⁵⁴. Nonetheless, for the quantum simulation of sophisticated topological lattices as described to be achieved in their full potential, fault-tolerant quantum computation, at the least quantum devices with vastly improved error characteristics and decoherence times, will likely be needed.